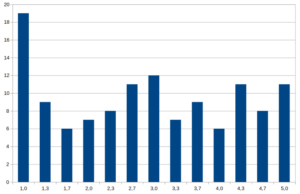
Theorie der Programmierung (SoSe 2023)

Klausurergebnisse

Vorlesungen

StudOn-Kurs

Termin Zeit Ort Dozent Beginn
Mo. 12:00 – 13:30 H7 Lutz Schröder 17.04.
Do. 14:15 – 15:45 H8 Lutz Schröder 20.04.

Intensivübung

Termin Zeit Ort Dozent Beginn
Mi. 14:15 – 15:45 K1 Paul Wild 26.04.

Tutorien

Termin Zeit Ort Dozent Beginn
Mo. 08:15 – 09:45 00.152-113 David Wegmann 24.04.
Fr. 12:15 – 13:45 00.152-113 Sebastian Dietlmeier 28.04.
Mi. 12:15 – 13:45 11501.04.023 Aaron Strahlberger 26.04.
Di. 08:15 – 09:45 00.152-113 Aaron Strahlberger 25.04.
Mo. 14:15 – 15:45 00.152-113 Leon Vatthauer 24.04.

Die Anmeldung zu den Tutorien erfolgt in der ersten Semesterwoche über StudOn. Beginn der Übungen ist in der zweiten Vorlesungswoche.

Bonuspunkte erhält, wer mindestens 50% der Punkte in den Hausaufgaben erreicht hat. Die maximale Anzahl an Bonuspunkten (also 6) gibt es bei 90% der Punkte oder mehr, dazwischen wird linear skaliert. Bonuspunkte können wie immer nicht zum Bestehen der Klausur führen, sondern lediglich zur Verbesserung der Note bei bestandener Klausur.

Die Abgabe der Übungen erfolgt wöchentlich in Gruppen von 3 bis 4 Personen. Die Personen einer Abgabegruppe müssen dabei nicht in der gleichen Übungsgruppe angemeldet sein. Dennoch würden wir Sie bitten, bei der Anmeldung möglichst der gleichen Gruppe beizutreten, damit wir den Korrekturaufwand gerecht auf die Tutoren verteilen können.

Wichtig: Die Abgabe erfolgt über den Briefkasten vor dem blauen Hochhaus. Vermerken Sie bitte auf der ersten Seite ihrer Abgaben stets die Namen aller Gruppenteilnehmer und den Namen des Tutors, damit wir die Abgaben den richtigen Tutoren zuteilen können.

Übungsblätter

Die Blätter enthalten Präsenzaufgaben für die Tutorien und bepunktete Hausaufgaben, die zum Erwerb von Bonuspunkten für die Klausur abgegeben und korrigiert werden. Die Übungsblätter werden auf StudOn veröffentlicht.

Klausur

  • Zur Klausur sind sämtliche papierbasierten Hilfsmittel zugelassen.
  • Wir empfehlen einen rechtzeitigen Blick auf die Probeklausur. (Die aber natürlich unverbindlichen Charakter hat, insbesondere garantieren wir nicht, dass alle Aufgabentypen aus der Probeklausur auch in der tatsächlichen Klausur vorkommen.)

Inhalt

  • Termersetzung
  • λ-Kalkül
  • Semantik von Programmiersprachen, Bereichstheorie
  • Induktion und Koinduktion
  • Reguläre Sprachen und endliche Automaten

Skript

Es gibt ein auf einer studentischen Mitschrift vom SoSe 2014 basierendes Skript (Stand 21.07.23), das im Laufe der Veranstaltung überarbeitet wird (siehe Revisionsnummern). Der Inhalt des Skripts ist während der Vorlesungszeit stets als vorläufig anzusehen, insbesondere hinsichtlich des Umfangs des Materials; will sagen, es kann ggf. Material hinzukommen. Eine Version, die dem tatsächlichen Ablauf der Veranstaltung entspricht, wird erst nach Abschluss der Vorlesungen zur Verfügung gestellt.

Literatur

Termersetzungssysteme

  • F. Baader, T. Nipkow: Term rewriting and all that, Cambridge University Press, 1999
  • J.-W. Klop, Term rewriting systems, in S. Abramsky, D. Gabbay and T. Maibaum (eds.), Handbook of Logic in Computer Science, Oxford University Press, 1992
  • J. Giesl, Termersetzungssysteme, RWTH Aachen, 2011

λ-calculi

Etc

  • G. Winskel, Formal Semantics of Programming Languages, MIT Press, 1993
  • J. E. Hopcroft, J. D. Ullman and R. Motwani, Introduction to Automata Theory, Languages, and Computation, 3rd ed., Prentice Hall, 2006
  • B. Jacobs, J. Rutten: A Tutorial on (Co-)Algebras and (Co-)Induction, EATCS Bulletin 42 (1997), 222-259.
  • J. Rutten: Automata and Coinduction (an exercise in coalgebra), Proc. CONCUR’98, LNCS 1466, 194-218, Springer, 2006.
  • P. Taylor: Proofs and Types, Cambridge University, 2003
  • M. H. B. Sørensen, P. Urzyczyn: Lectures on the Curry-Howard Isomorphism, 1998
  • A. Pitts: Lecture Notes on Regular Languages and Finite Automata, Cambridge University, 2013